Modeling coronavirus: duration of infectivity.

It is possible to try and perform simple curve-fitting to previous data to try and predict future values of total daily cases, deaths and so-forth, but this process wholly independent of plausible disease spread mechanisms and gives little insight into which control strategies might be most useful. As mentioned in the previous post, there are two variables that determine the shape of the coronavirus infection curve, and which enable us to make at least some ball-park predictions. One of this is at least partially modifiable by human intervention, and the other is not, being a function of the virus and resulting disease. The first of these variables is the related to the ease with which the virus is transmitted, and was previously denoted by the ratio D/N, where D is the number of daily cases and N is the number of total cases. This only works for simple models however, and more general approaches to this variable are needed. The second variable reflects the fact that in the real-world, each person infected with the coronavirus is only capable of transmitting the infection for a certain amount of time, which can be represented by an average for a large number of infections.

We model the daily change in infections by multiplying the ratio representing ease of transmission by the total active cases. The total active cases can be computed by subtracting the total number of cases T days previously for the current number of total cases, where T is the average number of days that an infected person is capable of transmitting the disease. This number should be approximately fixed, and can be inferred from actual data. When we do this, we can observe that the daily rate of change in the number of active cases (current day's active cases minus previous day's active cases with the difference divided by the previous day's active cases.) When we do this, we get a curve that looks like the following:

Figure 1.

We can compare the general shape of the curve with the actual daily new cases curve from South Korea:

Figure 2.

Figure 1 was generated simply from basic principles, i.e. that the intial spread follows an exponential profile, that the rate of growth depends n the number of presumed active cases, rather than total cases, and that the length of time that the average infected person can transmit the disease is limited.

If we look at the daily values for the D/N and the factor that we multiply by the number of active cases, we notice that two diverge the longer the epidemic continues. This is because D/N is computed using the total number of cases, and makes no allowance for the fact that the earliest cases are no longer capable of transmitting the virus. For this reason, we will replace the basic D/N, which works for purely exponential growth and is valid early in the epidemic, with a more general variable, r. Despite the change in variable and computation, r still represents the ease with which the virus is transmitted and can be modified by interventions such as social distancing, wearing masks, aggressive hand washing, etc. 

We can make two immediate observations: the number of daily cases will peak when the rate of change of the active cases crosses over the rate of change of r. The other thing to note is that there is a predictable tail, that represents the fact that there is initially an equilibrium reached where the number of daily new cases (the product of r and the previous day's active cases) and the rate at which previously infected persons become unable to transmit the virus.

Now that we have these basics, we can fit these curves to actual data, and model what would happen if r increased at certain points in the epidemic, representing relaxing of disease control efforts, what would be the effect of shortening the length of time a person remains infected, i.e. what if we had a cure, and what types of inferences can we make about r from the data obtained from other countries and states.

The simulation that produced figure 1 was implemented in Microsoft spreadsheet, and would take about 30 seconds to code in Exel. The details will be demonstrated in a subsequent post.

Modeling coronavirus

Modeling the SARS-cov-2 outbreak suggests that when the ratio of new daily cases in a region to the total number of identified cases in that region declines to a value of about 0.12 to 0.14, the daily number of new cases will consistently decline. Based on this, the number of daily new cases should be peaking in France anytime between now and sometime in the coming week. The number of daily new cases in New York should also begin to peak in the next one to two weeks.

Figure 1

Figure 1 represents what the daily number of new cases as epidemic beings to peak. The numbers on the vertical axis are not representative of a specific population and simply reflect the fact that the simulation was started with an arbitrary daily new case/existing case ratio of approximately 0.24.

Figure 2 represents a complete epidemic starting with a single case. The total number of infections for this simulation is 14,832 and the duration is approximately 135 days. Again, this represents a hypothetical population.

Figure 2.

Here are the principles behind the model, and the observations used to make predictions:

I. Exponential growth. 

The first quarter on the left hand side of the left hand side of the graph appears to represent an exponential function. These have the form N=N₀*(A)^t, where N₀ is the initial number of cases, A is some constant and t is the amount of time (usually in days) that elapses for the time that the number of cases was N₀. If the function is truly an exponential function then the rate of change of N is proportional to N. A is equal to 1+D/N where D is the number of new cases that occur during a day and N is the number of cases at the beginning of the day, or end of the previous day. If D/N were to stay constant, the number of cases would exhibit exponential growth, and soon, for a typical real-world ratio of D/N of about 0.2, the numbers would exceed the population of the earth in about 4 months. 

II. Real world growth.

Obviously, the number of infected people has not approached the population of the world. The value of D/N can be computed daily, and for the outbreaks in various countries typically begins at a value of about 0.4, then declines. Typical values right now are about 0.16 for the United States, 0.6 for Italy, 0.14 for France, and about 0.09 for the part of the world that is bothering to keep statistics. Values typical at the beginning of an outbreak are about 0.4, drops fairly rapidly to around 0.28 then more gradually to 0.22 after three weeks or so. The ratio of D/N can be thought of as the ease with with the virus spreads. If the virus spreads easily, the number of new cases will grow faster and D/N will be high. The opposite is true when D/N is low. D/N is noted to progressively decrease. This is because the virus has increasing difficulty spreading, because the uninfected portion of the population is, on average less susceptible than those already infected, and because of efforts used to discourage the spread of the infection. 

A model for the epidemic must account for declining D/N. The simplest way to do this is to assume that the number declines by a certain percentage each day. This is not rigorous, and there are more precise ways to do it, but for simple models it is adequate. If the number D/N were allowed to decay toward zero, the number of new cases per day would demonstrate a profile similar to Figure 3. The total number of cases would generate a sigmoidal curve shown in Figure 4.

Figure 3.

Figure 4.

This curve might allow for passable predictions. The graph above assumes an initial D/N of 0.4 and decays at the rate of 5% per day. This represents an optimistic increase in impairment to virus spread, and leaves out modeling crucial factors. Nonetheless, it does produce a reasonable shape for the the profile of new cases over time. At this point our model is N=N₀*(1+(D₀/N₀)*f^t)^t, where D₀/N₀ is the initial ratio of daily new cases to existing cases and f is the daily factor representing the decay D/N decreases, in the example 0.95. A more precise method would be to record actual D/N values and fit a polynomial curve using regression techniques.

III. Active cases.

One of the factors omitted from the simple model above is that only a portion of cases are contagious others have died or their infections have resolved. We should then adjust the model by replacing N₀ with each day's N_a, i.e. active cases. 

While D/N is a time dependent factor that decreases as a function of disease extent, and which can be intentionally modified with interventions such as social distancing, adjusting the profile of active cases is determined almost exclusively by properties of the virus and disease course. This fact is what makes disease limiting interventions work. It is the basis for estimating the time course of the disease and explains why the epidemic will die out long before everyone is infected. It also gives some insight into why a D/N of 0.4 may be the indicator of a resolving epidemic. This will be addressed in the next post.

Coronavirus: Modeling and prediction

To take the information we have available to us and construct a model that allows prediction of where the coronavirus epidemic is going, we need to determine two factors. These can be inferred from the reported data about the disease spread and represent the difficulty (or ease) with which the virus spreads and the average length of time an infected person remains contagious. These factors then can be used to construct a simple model that will produce a bell-shaped curve that is consistent with those representing other epidemics, as well as the experience in other countries during the spread of COVID-19. These models will be described and discussed in subsequent posts.

Coronavirus: A couple of thoughts on the model that limits infections in a non-immune population

The model described in previous posts, in which the portion of an exposed population that contracts an infection is dependent on the distribution of susceptibility and exposures, may benefit from a couple of points:

1.) While it may be the case that no one is completely immune, i.e. that they will not contract an infection regardless of their exposure, most people are relatively immune, i.e. they are more or less likely to contract an infection for a given exposure than someone else. Thus, as a theoretical matter, everyone can get the infection (although even if everyone were completely susceptible herd immunity would limit exposures) as a practical matter, for a given outbreak, the dynamics of how the disease spreads from more susceptible to less susceptible populations limits the extent of the epidemic.

2.) As per 1.) above, the uninfected population remains susceptible to infection given the right environment. Thus, a new epidemic, for example in the fall, is entirely possible, although it would likely have to start with a different set of dynamics. This distinguishes epidemics that are limited because a majority of the population has already been exposed from one in which the susceptibility to infection varies. Another distinguishing factor is that, in the latter population, a low level of infections continues, as for example occurred in Diamond Princess passengers.

3.) A population that has varying susceptibilities to infections appears somewhat abstract, and even though it makes sense to assume that not everyone has the same risk of infection given the same level of exposure, such differences seem far-fetched in real-world modeling. This is one way in which it might come about:

Assume that there are three dominant modes of exposure that transmit an infection: inhaling infected droplets, inoculating the oral or nasal pharynx directly, or by coming into contact with infected blood. The exposures representing the first type vary widely in the degree of associated risk. Passing through a room and breathing the air in the same room as someone with the infection is one degree of risk, but likely at a very low, almost negligible level. An intimate, hour long conversation within a foot of each each other a higher risk of the same type of spread, but one would assume that if a virus spreads easily just by breathing in infected air, is would be almost certain to infect the population to the level of herd immunity. Furthermore, we may assume that an individual's susceptibility to infection depends on personal factors: the type of viral receptors a person may have in his nasopharynx, which may in turn be affected by smoking status, medications, genetics, etc. It may be affected by anatomy or the quality of mucus or chronic inflammation. Regardless, we may consider that the population that is susceptible to infection by this route comprises the left hand side of the exposure-population curve. they are infected most easily and would be expected to contract the infection earliest in the epidemic.

The second group of people is relatively resistant to contracting infection just by breathing in. Although possible, the disease is unlikely to spread widely in this population simple by inhaling infected aerosol droplets. However, this group is susceptible to directly inoculating themselves by delivering virus directly into their oral pharynx, and especially their tongue, with virus they pick up on their fingers. A simple act of eating food with their unwashed fingers may be sufficient. Thus, while this group is more resistant than the previous one, it is still susceptible, and importantly, a large part of this susceptibility is behavioral.

The third group is very unlikely to contract infection by inhaling infected aerosols, and exhibit limited behaviors that predispose to direct inoculation from one's own hand. they are unlikely to become infected unless they come into significant contact with the infected bodily fluid; blood, sputum, urine etc. These people may be infected, but are very unlikely to do so.

Varying susceptibility to infection may be genetic, or come from partial immunity due to exposure to similar pathogens in the past, or because of co-infections that interfere with the new pathogen's ability to infect the host. Some people may simply have a better immune system.

Regardless of the case, if the first group of people, i.e. those who can be infected easily through aerosol spread is relatively small, and there is significant difference in the ability of the virus to establish infections between the two groups, the infection will spread widely in first group and begin to die out before it can establish a large enough presence in the more resistant populations to continue to spread.

Coronavirus: Interpreting the numbers

The daily coronavirus statistics have led to interpretations that pretty much span the realm of possibilities: It will infect 80% of the people; 80% are already infected; it will die out in warmer weather, it will not die out in warmer weather; It will get worse before it gets better; it will get much worse before it gets better; it is getting better; etc.

The month of March has provided significant data with which to consider the course and nature of the coronavirus epidemic. Significant events in March include peaking of the growth rate in South Korea, Flare up of the virus in Spain, and the dramatic flare in New York that began significantly affecting the data on March 13, 2020. What these data suggest is that:

1.) The virus does not spread easily. It is not that a whole lot of people are immune, it is more likely that there is a wide variation in susceptibility to infection among people who are not immune, presumably due to factors to be found in the upper airway and pharynx, rather than in the lungs.

2.) The risk of death depends not only on the risk of infection, but also upon the risk of pneumonia once infected. This likely involves a different set of risk factors.

3.) Most infections are not spread by airborne pathogens.

4.) The primary concern regarding "collapse of the healthcare system" is whether everyone who needs a ventilator has access to one. A key determinant of this is the length of time a person who requires mechanical ventilation remains on a ventilator, and these data are at least as important in forecasting severity of the epidemic as are total number of cases or deaths.

Coronavirus predictions

The data regarding coronavirus infections and deaths is still relatively scant, but is sufficient to make some observations and those observations allow crude predictions. Given the current state of the data the following predictions result:

1. The number of total infections in the United States in the first wave of infections will be approximately 400,000;

2. The number of deaths in the United States during the first wave will be approximately 5800;

3. There will be a second wave, that will not be as severe as the first;

4. Hydroxychloroquine will be found to reduce mortality by about 25%.

Rule of thumb for determining when the epidemic has peaked in an area: When the ratio of daily new cases to total cases, having previously gone above 0.3 drops to 0.14, and stays below 0.14 for three consecutive days. Note that the number of cases and deaths will continue to grow, but the epidemic will slow.

Coronavirus V: Chloroquine and hydroxychloroquine therapy.

New reports are full of references to chloroquine and hydroxychloroquine therapy. Such therapy is referred to as "experimental," "unproven," "promising," and so on. Some experts say it should not be used absent scietific data demonstrating its efficacy, others that it makes sense if a patient is in extremis; some suggest that it is a miracle cure, others that it is voodoo.

Hydroxychloroquine was developed as a less toxic version of chloroquine, Both are derivatives of quinine, a substance found in the bark of the cinchona tree. Natives of the Andean forests in which the cinchona trees grow chewed the bark to reduce shivering. When Jesuit missionaries arrived, they reasoned that patients afflicted with malaria shiver, and so perhaps cinchona bark might be used to treat malaria. Whatever the after-the-fact analysis of the underlying reasoning, it turned out to be correct. The active ingredient in cinchona bark was found to be quinine, and British military health authorities developed tonic water for use by British forces in malaria stricken areas. Quinine can have significant aide effects, and so scientists sought ways to modify quinine to make it less toxic. Choloroquine and hydroxychloroquine resulted from these efforts. Clinical observation subsequently found that hydroxychoroquine seemed to be therapeutic in rheumatoid arthritis and lupus. Its efficacy has been proven in these conditions. Chloroquine was also thought to demonstrate some antiviral activity, and even to treat diabetes.

Obviously, cholorquine and hydroxycholorquine seem to be beneficial in a number of disparate conditions, and this implies that they have a number of effects within the body. Their antmalarial effect is thought to be due to alterations in hemoglobin metabolism, allowing toxic heme to accumulate inside the parasites, poisoning them. The benefit in rheumatoid arthritis and lupus is thought to involve downregulation of Toll-like receptors, modifying immune response. The antiviral effects are thought to involve proton trapping within cell lysosomes, altering cell pH. Another theory is that the drugs facilitate entry of zinc into cells, and zinc inhibits viral replication. That is quite an array of effects. They likely share the common factor of altering enzyme function, possibly through affecting intra-celluar acid-base balance.

The suspected activity in coronavirus infection is that they alter acidity within human cells, and many enzymes essential for viral replication are pH dependent. Thus, use of chloroquine and hydroxychloroquine to treat coronavirus infections is rational. That is, there may a reason to think that they will work. Furthermore, there is some evidence, certainly not determinative or scientific enough to establish the efficacy of chlorquine or hydroxychloroquine in treating viral infections, that they are beneficial in treating coronavirus infections. Nonetheless, such evidence supports the empirical use of these medicines in COVID-19 cases.

Both empiric therapy e.g. giving antibiotics to someone with a fever and elevated white blood cell count, but no obvious source of infection, and rational therapy, e.g. treating hepatic encephalopathy with lactulose, are well accepted in modern medicine. Thus, the fact that the benefits of either choloquine or hydroxychloroquine in treatment of COVID-19 have not been proven are not particularly strong arguments against their use. Furhtermore, in severe COVID-19 disease and ARDS, it may be immune-modifying effects that have been demonstrated in rheumatoid arthritis and lupus that is most beneficial. Such effect may mitigate the lung injury caused by the immune response.

Both chloroquine and hydroxychloroquine do have potential adverse effects. The most concerning are provocation of heart arrhythmias and visual impairment. These are the risks that need to be considered in risk/benefit analysis. The fact that neither chloroquine nor hydroxychloroquine have been scientifically proven to benefit COVID patients affects the potential benefits. Nevertheless, a reasonable analysis can occur and a valid decision to use one or the other can be reached. At this point, it would seen that chloroquine and hydroxychloroquine do have a place, although an admittedly uncertain one in patients with COVID-19, especially those with limited options.

Coronavirus IV: Hypothesis as to what process limits the numbers (continued)

As mentioned in the last post, the phenomenon discussed there is a way to explain why the portion of a population that is ultimately infected by a pathogen may be less than "almost everybody." It is noted that this approach does not inform as to what is going on day-to-day. Here is a model (again a model, not a description of a a biologic process) that results in epidemics petering out prior than they would otherwise be expected to.

First, we should consider how the quantity that was previously described as "exposure" changes as an epidemic progresses. It seems reasonable that the more people infected, the more exposure there is for everyone else. It may be that the amount of exposure increases exponentially with the number infected, linearly, logarithmically, and so on. It is important to note that we are not talking about exposure per time (which would be expected to be exponential if plotted against time) but exposure as a function of the percentage of the population infected. For purposes of explaining the concept the actual relationship does not matter, so we will assume that each infected person generated the same number of exposures, i.e. that the relationship is linear.

If we graph exposure versus percent of the population infected then, we get a line, and we also get a line if we instead graph corresponding percent of the population infected versus exposures. Now we have the same axes as Figure 1 from yesterdays chart.

Next, we want to graph the cumulative portion of the population from Figure 1, that is integral or sums of the total population as we go from left to right. This is the same process used to generate cumulative distribution functions in probability and statistics. We can plot this on the same chart and if we just retain these two new curves we get something like the following:

The red line is cumulative population distributed according to amount of exposure associated with infection, and the green line is the amount of exposure as a function of the population infected. Here, it is useful to think of exposure as an environmental variable. In reality, it is not likely to be evenly distributed, but this fact does not affect the principle to be illustrated.

The important thing to note is that on the left hand side of the chart, the red line is above the green line. We can use the fact that we have plotted the two curves on teh same chart to obseerve the following: for a given percentage of the population we can compare the amount of exposure associated with infection in the population to the amount of exposure associated with the percent of the population infected. We can observe various scenarios as illustrated:

Here we see that at a Percentage of population of 23% the amount of exposure is greater than the exposure associated with infection (or more accurately, the percentage of the population capable of transmitting the infection) in that portion of the population. There is therefore, excess exposure and the contagion will continue to grow. Conversely, if we move up to 52%. we see that the green line is above the red line and at that point the amount of exposure is less than the exposure associated with infection. Everyone whose risk of infection requires exposures greater than that produced by the current percentage of the population infected is less likely to become infected. Therefore the contagion will slow significantly, and as fewer people remain capable of transmitting the infection, will decrease. The vertical green line will begin moving back to the left as the percentage of the population capable of transmitting infection falls, but as it does so, it is moving back into a portion of the population that has already been infected. The epidemic will therefore drop off rapidly, creating the bell-shaped curve described by Farr.

The interesting point is that at which the red and green lines cross. This is the point where the epidemic peaks, and where it is located is a function of how susceptibility and exposure is distributed in a population. The point of cross-over may be at a very low percentage of the population in which case, the numbers observed for the Diamond Princess and San Marino may not be as exceptional as they seem. As mentioned in the previous post, these distributions can be affected by public health interventions, and are more likely to be significant as the two curves described above begin to cross.

These models make several assumptions. The first is that not everyone has the same susceptibility to infection, even at the same level of exposure. The second is that people do not remain capable of transmitting the infection indefinitely, but in a large number of infected people, the mean duration of infectivity is adequate to provide a useful model. The third is that the distributions of the exposures and risks are to some degree modifiable. The last, and most important, is an observation, more or less universal that applies to all types of systems: electrical, mechanical, chemical, economic, political, ecological, etc. That is that stable systems seek points of equilibrium. In the case of an epidemic, if that point exists at a number of infections greater than those currently existing under current conditions, the epidemic will grow until that point is reached. If the number exceeds the point of equilibrium, the epidemic will slow. If people remained infectious forever, and did not develop any immunity, the epidemic would find teh point of equilibrium and persist, but because people are only infectious for a limited time, and likely develop some degree of immunity once infected, the epidemic ends.

Coronavirus: Attempting to explain the Diamond Princess and San Marino, continued.

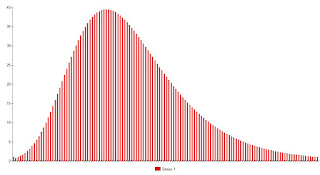
The previous post illustrated the concept of "exposure." It was modeled as an aggregate of encounters that have varying probabilities of transmitting an infection. In the simple case modeled, it was a function of number interactions and the probability of transmitting the disease with each interaction. As mentioned there, these variables are expected to vary from person to person. One person may contract the infection from a low risk encounter, such as using a self serve gas pump after an infected person, or conversing with an asymptomatic infectee from a few feet away. Other people will not become infected despite higher risk exposures. To model this for a population, it is sufficient to create a parameter called "exposure." This is an aggregate of number of exposures, risk per exposure, and individual susceptibility to acquiring infection. In theory, if we could measure and keep track of "exposure" we could derive a detailed epidemiologic model. However, for he sake of illustrating concepts it is sufficient to create an arbitrary exposure profile and illustrate how that affects infection rates. For the sake of illustration, the following figure plots the number of people who acquire an infection against the minimum exposure required to do so. People highly susceptible to infection are on the left hand side of the curve, relatively immune, or those more resistant to infection are found on the right. For example, the first bar on the graph indicates that .004 % of infections for this hypothetical virus occur in people who have the lowest level of exposure, arbitrarily deemed 1 unit; 1.2 percent with an exposure of at least 2 units, etc. The graph is scaled so that the sum of the percentages is 1, representing the entire population that contracts the disease.

Figure 1.

The shape of this particular curve is arbitrary, created merely for illustrative purposes.

Now it would be useful to know how exposures are distributed throughout the at-risk population. To do this, we can plot the percentage of the population that experiences a given exposure. We may get a plot that appears as follows, again created for illustrative purposes only:

Figure 2.

And we can plot them on the same chart:

Figure 3.

The idea to be illustrated here is that the distribution of exposures may differ from the distribution of susceptibility in the population, and this will determine the final percentage of the population that is infected, even if no one had previously been exposed to the disease. Again the key point is that not all exposures have the same probability of passing the infection, and not all people have the same probability of becoming infected from identical exposures. After going through this analysis, we arrive at a common sense conclusion: the fewer exposures that occur in people more resistant to infection, the smaller the percentage of the population that will become infected.

Here is a highly schematic example:

Assume tht we have 300 people. 100 are in the less resistant (more susceptible) group, 200 in the more resistant group. Now let us assume that among these 300 people there are a total of 600 exposures. Each exposure is associated with a 0.5 probability of transmitting infection. Further assume, for purposes of illustration (the purpose is to illustrate the effect of differential distribution, not practical epidemiologic modeling) that these exposures are evenly distributed, so that everyone experiences approximately 2 two exposures. Each person has a 75% chance of being infected (1-(1-.5)^2), so the expected number of infections throughout the population is 300*0.75=225.

Now assume that the exposures are unevenly distributed. Assume that of the 600 exposures 400 occur in the less resistant group and 200 occur in the more resistant group. Again, assume that the exposures are evenly distributed. Now the expected number in the less group is 100*(1-(1-0.5)^4)=94 infections, and in the more resistant group, it is 200*(1-(1-0.5)^1)=100 infections. Now the total number if infections is only 194, rather than 225. This result is due only to redistributing the exposures. It should be noted that, so far "less resistant" and "more resistant" are only labels. Each group, as modeled so far has the same susceptibility sine the risk per exposure is 0.5 in both groups. To justify the labels the probability of infection in the lower resistant group has to be higher than that in the higher resistance group. For the sake of illustration let us keep the probability in the lower resistance group 0.5 but make that in the higher resistance group 0.4. Now the expected number of infections in the higher resistance group is 200*(1-(1-0.4))-80, and the total number if infections is now 174.

We can apply a similar model to the distributions given in Figures 1, 2 and 3. For assumed baseline numbers with a the highest probability of infection per exposure of 0.75, that everyone is equally susceptible and that exposures are evenly distributed, the expected number of infections in a population of 1000 people is 996. For the distributions in Figure 3, assuming a predictable decrease in the probability of infection as we move to the left on the graph, the expected number of infections in the total population is 522. If we swap the profiles, so that the green distribution represents the percent infected as a percentage of risk and the red the distribution represents the distribution of "exposure," the expected number of cases in the population predictably increases to 740.

Again, this just applies numbers to what should be a common sense phenomenon. If we shift the curve of percentage of the population infected as a function of exposure (Figure 1) to the right, and Figure 2 to the left, the total number of infections will go down. In other words, if fewer exposures occur in people who require more exposure to become infected, even if the total number of exposures remains the same, the final number of infections will decrease.

As a practical matter, the red curve is shifted to the right by decreasing the probability of transmission per exposure. The total area of the curve of figure 2 is decreased by minimizing exposures, social distancing, avoiding gatherings, regularly decontaminating surfaces, etc.

A limitation to this type of model, is that merely tries to explain why the total number of people infected during an epidemic is less than 100%, or even the portion arrived at by considering "herd immunity" as the limiting process. What this does not do is account for the expected increase in the amount of the quantity that we simply called "exposure" as the number of cases increases, nor does it give any insight into how an epidemic proceeds over time. That will be addressed in another post.

Corona virus III: a hypothesis to explain the Diamond Princess and San Marino data.

The number of passengers on the Diamond Princess cruise ship that were infected with the Wuhan coronavirus (SARS-cov-2) is perplexing. Why wasn't everyone, or nearly everyone infected? Michael Levitt, a Nobel-prize-winning researcher from Stanford University surmised that immunity to the virus is more widespread than thought. This is a workable explanation to a point, but does not explain why people are immune. Perhaps previous non-SARS coronavirus exposures conferred some degree of immunity. Maybe some people are just naturally immune, and maybe a little of both. This post and a couple of those that follow suggest how the proportion of a population that has little or no previous exposure to a virus can end up with an infected population that is only a fraction of the total population. From this, we can formulate a model that fits the existing data from the Diamond Princess, San Marino, South Korea, Washington state, etc. to get a prediction of how extensive coronavirus infection will be, as well as how we can recognize when the epidemic is receding.

To begin, here is a simple thought experiment to help establish some ideas:

Assume that there are two men on an island, and one of them becomes infected with a disease from someone who temporarily visited the island, but is now gone. Assume also that the other person on the island is not immune to the disease, and that the infected person can transmit the infection for only a limited time, for the sake of simplicity, say one day. Now assume that the uninfected and infected person encounter each other regularly, say, four times a day, and that during each one of these encounters the risk that the uninfected person will contract the infection is p=1/6. If the risk of infection from a particular encounter is independent of previous encounters, which is reasonable, then the risk that the uninfected person becomes infected during the time the infected person is capable of spreading the infection is

Pi=(1-(1-p)^4); = (1-(5/6)^4); = (1-0.482);
=0.528

Thus, under the schematic circumstances described above, the uninfected person has an approximately 53% chance, or slightly more likely than not, of becoming infected. If he alters his interactions with the infected person and spaces out his interactions so that the two now encounter each other only three times during the period the infected person can transmit the virus, the risk that the uninfected person will catch the infection is

Pi=(1-(1-p)^3); =(1-(5/6)^3); = (1-0.5787)
=0.4212.

Now the probability that the uninfected person becomes infected is only 42%; more likely than not that he will NOT that he will not become infected. Note that the number of exposures was decreased by 25%. If instead, we decrease the risk of exposure by 25% so that p is now pn=1/6*(3/4)=1/8, and we still have the original four interactions, the risk of infection is now

Pi=(1-(1-pn)^4); =(1-(7/8)^4); =(1-.586)
=0.413.

Decreasing the risk per exposure reduces the overall risk of infection by a little more than a proportional reduction in the number of exposures.

The key concepts illustrated by this thought experiment are that:

1.) The amount of time that an infected person can pass along the infection is limited;
2.) The risk of infection depends on the nature of the interactions that produce exposures;
3.) Modifying exposure risk decreases the likelihood of disease transmission, even when the risk of transmission is not completely eliminated.
4.) An exposed person may not become infected even if not immune.

These concepts should be easy to understand. Not all exposures carry the same risk of infection, for example, not everyone who shakes hands with an infected person will become infected, nor will everyone who passes an infected person on the street. It is understood as well, that apart form the artificial constraints imposed by having only two people on an island, an uninfected person is likely to have multiple encounters with many infected people, but the underlying principle is the same: each such encounter is associated with a risk of infection that is greater than zero but less than one. In the next post, the concept will be generalized to illustrate how the final number of people infected in a population will tend to a value other than 100%.

Coronavirus II

There are two key locations, the data for which are instructive for analyzing the Wuhan coronavirus epidemic. The first is the Diamond Princess cruise ship. That vessel had approximately 3600 people on board when the outbreak occurred and presumably everyone on board was exposed. Yet, only about 20% were diagnosed with COVID-19. The other relevant locale is the Republic of San Marino. That is a very small (24 square mile) sovereign state located 200 miles from Milan and completely surrounded by Italy. Its population is about 33,300 and like the Diamond Princess, it is reasonable to assume that almost all have been exposed. There are 144 cases of COVID-19 there at this time.

If Italy, the country hardest hit by corona virus experiences continued exponential growth, at the same rate, it will reach the same relative prevalence of COVID-19 as San Marino on about April 1, 2020.

The daily new cases as a percentage of existing cases is currently 15% in Italy, 2% in New York state, 10% in Washington state, and 1.8% in South Korea.

An informal interpretation of the above is that approximately 5% of the population is susceptible to clinical infection (symptomatic) under "typical" exposure environments, approximately 20% under "intense" exposure environments and approximately 1% under "precautionary" exposure environments. Likewise, the corresponding new/existing case rations are about 43%, 75% and 12% respectively.

Coronavirus

Here is another way of thinking about the course of the Wuhan coronavirus epidemic. It is common to refer to the R0, i.e. the number of persons infected by a person who already has the disease. An alternative, that seems to match the experience of certain countries that have experienced significant COVID-19 cases is as follows.

Rather than try to estimate how many persons are infected by each already infected person, assume that each case will transmit the disease to two other persons, x number of days apart. It makes sense that the harder it is for the virus to spread, the longer the interval between transmissions. Thus, the number of days that it takes an infected person to infect two others gives a measure of how effective interventions to slow the virus are. The calculation is also very straightforward.

If we assume that a person becomes infected, then infects someone in x days, and another person in an additional x days, then no one else, the growth in the number of cases follows a modified Fibonacci sequence, but the ratio of the number of cases the previous day to the present day is the same as the Fibonacci or "golden ratio," i.e. 0.618. (The Fibonacci sequence will give 121393 cases in 25 days assuming daily transmission; the one patient-two-transmissions in 2x days gives 196417 cases in 25 days).

When the virus has broken out in a country before containment measures have been instituted the ratio of new cases to known previous cases is approx 0.45. This implies that each infected person infects two people about 1.37 days apart. (It is also possible to create similar models in which an infected person infects three other people y days apart, four other people z days apart, etc., but it does not affect the underlying analysis. The important point is that as spread of the virus is impeded, the number of days between transmissions increases.)

This approach is justified when the graph of logarithm of cumulative cases approximates a straight line. It implies that the growth in the number of cases is exponential, as is the case with the Fibonacci sequence (N~N0*(1+.0618)^t). In other words, if the logarithmic graph of cases is linear, the disease growth is behaving as expected.

Now we can make the following observation. If we look at the countries that have had a significant number of coronavirus cases, South Korea and China seem to have gotten control of their epidemics, and Taiwan's seems not to have gotten out of control. Here is the interesting thing: The growth in the number of cases seems to have reversed in China on February 4, 2020, and in South Korea on March 1. 2020. In both cases the calculated "x" was about 2.8 days. Again, this is not a real-world number. It is a statistical surrogate for the difficulty involved with transmitting infection between one person and another. It likely reflects a number of factors: how long the virus can remain infective on fomites, the "distancing" between persons in a population, infection control procedures, etc. It should also be noted that the number of 2.8 days occurs when the daily number of new cases is approximately 19% the number of previous day's cases. This does not mean that the number of infections stops or that the epidemic is over; it does suggest that when x=2.8, the number of daily new cases is about to peak.

Of note, in the United States currently, the number is approximately 2.16 days. In Italy it is 3.1, implying that Italy's number of new cases should start to decline.

It is also important to note that this number reflects difficulty in disease transmission depending on the current environment, with current precautions and behaviors. It is not an indication of how the virus will behave if the environment, e.g. containment measures, etc. change.

The number 2.8 (actually 2.77) days is not a scientific constant. It does however have the benefit of quantifying the state of an epidemic against an intuitive metric. It is reasonable that if x is greater than the number of days an infectious person can pass along the disease, the epidemic will die out. But there is some subtlety involved. It is not unreasonable to consider a variable I, which can be thought of as the transmissibility of the disease. It is also not unreasonable to think that this number is constant, starting at some time after infection and abruptly dropping to zero at some later time, indicating the that person is no longer capable of transmitting the disease. Rather it is reasonable to assume that the value I follows a bell-shaped curve over time, reaching a peak at some point, and being highly unlikely to support disease transmission at the tails. The profile of I in a given person is likely to be a factor of the person and the virus, and to be stable over time. If the amount of time required to infect an additional one or two people (from the time the person becomes capable of transmitting the infection, not when he becomes infected) increases, the likelihood of disease transmission goes down, and at a certain point, the epidemic stalls. This is true even in the absence of "herd immunity," or other disease-limiting processes.

Healthcare and the limits of the free market

While it is undeniable that free markets and competition are efficient optimizing mechanisms in general, their place in a system of healthcare is more complex. There are several reasons for this.

A clear example of how competition is a mechanism for selecting the best of something is a sports tournament bracket such as the NFL playoffs or the NCAA men’s basketball tournament. At each point in the bracket, i.e. each game, the “better” contestant is selected and advances, resulting, in theory, that the winner of the last contest will have been the best. The tournament and competition is a process of progressively determining “better.” In these circumstances however, the criteria for what constitutes better and best are obvious. The games are played according to rules that apply to all games and the criteria for determining successful outcomes does not change from one contest to the next. Coaches and managers can strategize and game-plan and improve according to the accepted criteria for success. This concept does not translate cleanly to healthcare. There are not accepted criteria, analogous to game rules, objectives or criteria for winning, that are generally applicable to healthcare. For example, given a group of possible treatments for a given condition, different people will have different perspectives on what constitutes “better.” Some patients are afraid of needles, some would rather tolerate the disease than the cure, others have idiosyncratic biases for and against certain treatments (for example, “natural” or “homeopathic” cures). Some treatments are associated with longer recovery times, or are more painful or more disfiguring, and have different efficacies that different people value differently. It is hard for markets and competition to select out better processes if there is no clear idea of what “better” is. (One anticipated response is that markets allow people to select what is better for them, and thus, within defined subpopulations there is a workable idea of what is better. This is true regarding subpopulations, but the word “system in the first paragraph was chosen intentionally. Unless those subpopulations are self-contained, optimizing outcomes within those populations does not necessarily improve the system as a whole.)

Another challenge for markets is the tension between “best” and “good enough.” The whole idea behind competition is to determine what is best. The whole idea behind the give-and-take of healthcare policy is to determine what is good enough in the setting of conflicting interests. There is little doubt that if the priority of healthcare policy were to minimize the risks of medical penury, competition would find a way to achieve that outcome, but at the expense of other considerations. The same applies to cost-effectiveness, affordability, access, universal coverage, innovation, etc. Different constituencies have different priorities, and as competition optimizes one, it will likely burden another. When this happens, expect the “losing” constituency to complain that the healthcare system is broken, and that the government must fix it. Here is the general principle: competition is concerned with what is best; policy-making is concerned what is good enough in the setting of conflicting interests. Competition is still the optimizing mechanism in both cases though, except in the policy-making case it is competition for political influence, not healthcare outcomes.